Полосовая модуляция – это процесс изменения одного или нескольких параметров высокочастотного (ВЧ) несущего колебания по закону низкочастотного сигнала. Передаваемая информация заложена в управляющем (модулирующем) сигнале, а роль переносчика информации выполняет высокочастотное колебание.

Откуда возникло слово полосовая? Существуют и другие виды модуляции, например широтно-импульсная модуляция (ШИМ). Она к полосовой модуляции не относится. К полосовым относится модуляция ВЧ колебания. Если рассмотрим спектр, то у ШИМ спектр будет прижат к нулю частот.
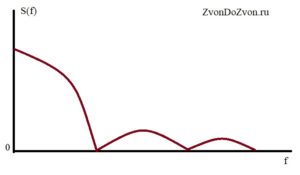
А если рассмотрим спектр полосовой модуляции, когда модулируем ВЧ колебание, то спектр будет занимать определенную полосу. Спектр будет концентрироваться возле частоты несущей. Передаваемая информация закладывается в том параметре, который мы изменяем, это либо амплитуда, либо частота, либо фаза.
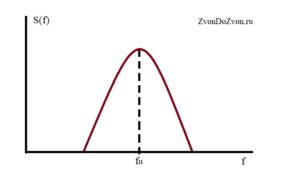
Будем отличать модуляцию и манипуляцию. Манипуляция это в принципе та же самая модуляция, но когда у нас модулирующий сигнал, низкочастотный (НЧ) сигнал, который изменяет параметры, имеет дискретный (цифровой) характер.
На картинке ниже два отличия. Модуляция, когда модулирующий сигнал, который изменяет амплитуду аналоговый, т.е. непрерывный, а справа модулирующий сигнал, который изменяет амплитуду цифровой.
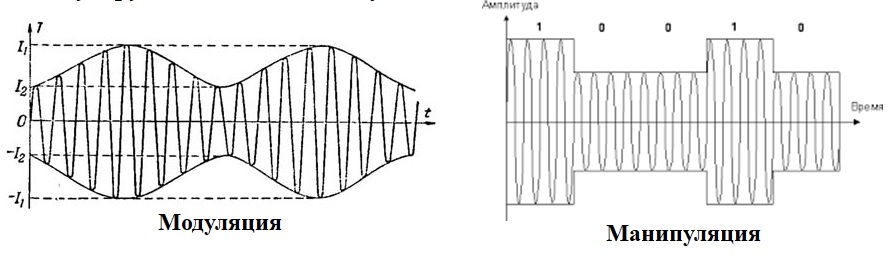
Когда мы говорим про манипуляцию, модулирующий сигнал имеет дискретный характер. Но когда мы говорим модуляция, то это не всегда означает, что модулирующий сигнал аналоговый. Например, квадратурно-амплитудная модуляция (КАМ), не смотря на то, что там модулирующий сигнал (т.е. тот сигнал который несет информацию, который изменяет параметры ВЧ колебания) он цифровой, но все равно называют модуляция.
Постепенно будем переходить от формы записи гармонического колебания с модуляцией к другой записи. Модулированный сигнал в общем виде можно записать следующим выражением: s(t)=A(t) cos(θ(t))
- А(t) – закон изменения амплитуды от времени;
- θ(t) – закон изменения мгновенной фазы от времени; мгновенную фазу можно расписать: θ(t) = ω0t + φ(t)
- ω0 – угловая частота несущей: ω0 =2πf0
- φ(t) – закон изменения фазы несущей.
- Если изменяется A(t) гармонического сигнала – то модуляция называется амплитудной;
- Если изменяется θ(t) – то модуляция называется угловой. К угловой относятся частотная и фазовая модуляция.
Комплексное представление гармонических сигналов
Теперь мы гармонический сигнал s(t)=A(t) cos(θ(t)) будем постепенно преобразовывать. Гармоническую функцию cos заменим на комплексную экспоненту. Это экспонента, в аргументе которой есть мнимая единица i.
Комплексная экспонента расписывается по формуле Эйлера e^ix=cosx+isinx.
Мы видит, что эта комплексная экспонента, тоже гармоническая функция. Если вместо х подставим t и подадим ее на осциллограф, мы увидим синусоиду и косинусоиду, сдвинутых относительно друг друга на 90 градусов.
z(t)=A(t)(cosθ(t)+isinθ(t))
Заменим гармоническую функцию cos на другую гармоническую функцию комплексную экспоненту z(t)=A(t)e^iθ(t)=A(t)e^(ω0t + φ(t)).
S(t) вещественный сигнал, а Z(t) аналитический сигнал. Они между собой не равны, но из аналитического сигнала, можно получить вещественный сигнал. Нужно будет оставить действительную часть, а мнимую отбросить s(t)=Re[z(t)]=Re[A(t)e^θ(t)].
Зачем нам переходить от привычной записи в вещественном виде к комплексной?
- Позволяет оперировать сигналами с полосовой модуляцией, не учитывая частоту несущей.
- Позволяет перейти к векторному представлению сигналов и простому описанию ФМн и КАМ сигналов.
Умножение сигнала z(t) на e^iφ приводит к повороту фазы сигнала на φ радиан. Умножение сигнала z(t) на e^iωt приводит к изменению частоты на ω рад/с.
Продолжение Вы найдете на сайте ZvonDoZvon.ru в разделе радиосвязь.


